Tool: Solving containers

Looking at an entire row, column or box

---

<< Return to techniques page

Next technique: solving sections >>

Introduction

Sudoku puzzles cannot have the same number twice in any row, column or box (container). You can take advantage of this by using deduction to determine (1) which numbers are missing, and (2) where the missing numbers go.

Details

When you see a row, column or box that is only missing one number you know what that number is and you can fill it in. This is the most basic use of this technique. You only need one container to illustrate this, as in this row example.

This row is only missing one number and it is a 3. You can fill it in.

You can do the same thing with multiple numbers missing in a container. But as the number of empty cells increases the ability to find numbers decreases, and you need numbers in other adjacent containers to help you know which numbers are missing. Here is a row with two numbers missing.

It is pretty easy to see that this row is missing a 1 and a 3. The cells in column one and four are the empty ones. So far no rocket science here. In order to fill these two numbers in you must know where at least one of them goes. If there is a 1 or a 3 in either column one or four (or in box one or two) you would know how to complete the row.

Now let's look at a formula.

Formula

This is kinda like math but don't get nervous. It's not too hard to grasp. To solve any number of empty cells in a container where n is the number of empty cells, you need to have n-1 known numbers outside of that container to solve one of the empty cells. Stick with me - here's an example.

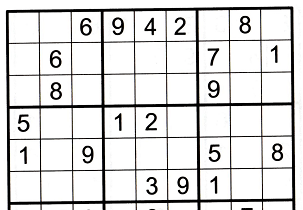
Look at row one in the above image. It has four empty cells. The missing numbers are 1, 3, 5 and 7. So n is 4 and n-1 is 3. That means we need n-1 (three) known numbers to solve one of the n (four) empty cells in row one. Once one cell is solved n becomes 3 and n-1 becomes 2. And so on until we have only one cell left to solve. At that point n is 1 and n-1 is 0. Or in other words we need to find zero numbers to solve the last cell (because it's the only number left for that row).

Look at column seven. It has the numbers 1, 5, 7 and 9 in it and they are all outside of row one. 1, 5 and 7 happen to be three (n-1) of the four (n) numbers we're missing. So that tells us row one column seven is a 3. Good job!

After the 3 is filled in we have three (n) empty cells left so we need two (n-1) known numbers to solve the next empty cell. You'll notice that column one has two of the three needed numbers in it (a 1 and a 5), and therefore a 7 goes in to row one column one.

Each time you fill in a number n and n-1 go down one number. With this knowledge you can now finish solving row one.

This video illustrates the concept of solving containers.

Skill Levels

This technique can be used for any level of difficulty. If you're only missing one or two numbers it can be easy to use.

There are times when you only have one or two known numbers in a given container. This can help you find numbers. But it is tricky to do if there aren't many numbers yet. This is a more advanced tool when there are fewer numbers in a container.

Next technique: solving sections >>

<< Return to techniques page

---