Sudoku Glossary of Terms
Understanding the sudoku terminology on this page will help you both on this website and in other places that discuss sudoku. A quick review of these sudoku concepts will help you understand what is meant as you run across the differnet terms.
Use this page to become familiar with the terms on this site. You can refer to it when you see a term you don't understand. It is recommended that you at least skim through the list of terms and read the ones you aren't familiar with so you recognize them when you see them.
Bowman's Bingo
Sudoku Bowman's Bingo is is a sudoku technique where a solver uses trial & error to find the correct number in a given cell. A number is placed in a cell that is assumed to be the correct number, then it is checked to see if that choice causes an error in another part of the grid. See also nishio.
Many solvers frown upon trial and error strategies.
Sudoku Box
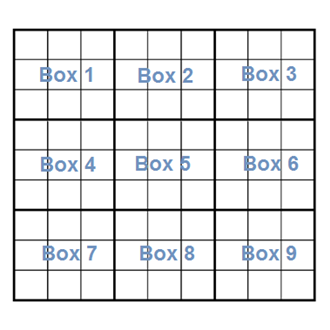
A sudoku box is a series of nine cells organized in three rows and three columns within the box. The sudoku grid has 81 cells with nine overlaid boxes (three wide and three high). Boxes are numbered from the top left (box 1) to the bottom right (box 9). See also numbering. Boxes are one of the three container types. See also container.
Sudoku Candidates
Writing candidates is a sudoku notation scheme where numbers in each cell are written to keep track of each possible number for the given cell. Some or all candidates can be written but writing all candidates is both time-consuming and messy. Snyder Notation is a modified way of writing some candidates that is superior to writing all of them.
Candidates are also often called pencil marks, and sometimes called little numbers.
Sudoku Cell
A sudoku cell is the smallest unit in a Sudoku puzzle. A cell is a "bucket" that can hold one number. There are 81 cells in a sudoku grid.
Sudoku Column
A sudoku column is a vertical series of nine adjacent cells. Each column holds the numbers 1 through 9. Every number exists in each column and no number repeats. Columns are one of the three containers.
Sudoku Container (also Sudoku House)
A sudoku container is a group of cells that holds (contains) an entire set of nine numbers. There are three types of containers - rows, columns and boxes. See row, column and box on this page for an explanation of each of these container types. See also container numbering.
Fully Symmetrical Sudoku Puzzle
If a puzzle can be flipped horizontally, vertically and rotationally, and still have numbers in all of the same cells, it is considered fully symmetrical. See Rotational symmetry below for a symmetry explanation. Rotationally symmetrical puzzles may not keep their symmetry when flipped horizontally or vertically. But if they do, they are fully symmetrical. The example images in the rotational symmetry section below are not fully symmetrical.
Sudoku Givens
All standard sudoku puzzles start out with numbers that are already filled in by the puzzle creator. These numbers are called sudoku givens. These givens are clues that help you find the rest of the numbers.
Sudoku puzzles have nine rows and nine columns which gives 81 total numbers. Research shows that a puzzle must have at least 17 givens. If it has less than 17 givens there will be more than one solution.
Easier puzzles generally have more givens and harder puzzles have fewer. However the skill level of a puzzle is not entirely determined by the number of givens.
Sudoku Book for Programmers! > >
Sudoku Grid
A sudoku puzzle has 81 cells, organized in 9 rows and 9 columns. 9 boxes overlay the 81 cells. This organization of cells is called the sudoku grid.
Sudoku House
A sudoku house is a container that holds all numbers (1 through 9). A house can be a row, column or a box.
Howard Garns
American Architect and puzzle creator, inventor of sudoku.
Howard Garns created what is known today as sudoku. He invented "Number Place," the original name for sudoku, while working for an architectural firm in Indianapolis, Indiana. Number Place was published by Dell Pencil Puzzles and Word Games in May of 1979. He isn't officially known as the inventor of sudoku, but his name appeared in the list of contributors in the Dell magazine in each issue that included Number Place.
Number Place didn't really catch on until Nikoli, a Japanese puzzle publisher, found the puzzle and started creating and publishing rotationally symmetrical Number Place puzzles. Nikoli named the puzzle sudoku.
Maki Kaji
Maki Kaji was the president of Nikoli Publishing, and is widely known as the "father of sudoku" because his company made sudoku popular in Japan. Mr. Kaji passed away in 2021.
Sudoku Nishio
Sudoku Nishio is a trial & error technique. A solver finds a cell where s/he knows there are only two candidate possibilities, chooses one of the two, and continues solving. If the chosen candidate is correct, the puzzle will be completed with no conflicts. If the wrong candidate is chosen, one or more conflicts will appear. See also Bowman's Bingo.
Sudoku Notation - cells, rows, columns, boxes
When people communicate about sudoku they need a way to describe it in text form. When a cell is specified, or when certain combinations of cells are described, a shortcut notation is used to specify its location. This shortcut notation is explained here.
What does r2c3 mean?
A single cell is called out by specifying its row and column numbers with an 'r' preceding the row number and a 'c' preceding the column number. Examples: r1c9 means the cell in row one and column nine (the rightmost cell on the top row). r8c3 is the cell on row eight, third cell from the left. Hopefully this is straight-forward and easy to understand.
Rows are specified by their number and columns are called out by their number. Row one is the top row, row nine is the bottom row. Column one is the leftmost column, column nine is the rightmost column. Boxes use the same numbering as rows and columns. box one is the top left box. box five is the very middle box, and box nine is the bottom right box.
Index of YouTube sudoku videos > >
Sudoku Numbering
The Sudoku grid is numbered to aid in illustration when explaining concepts. The three containers are each numbered 1-9. The illustrations below show how each container is numbered. This should be very straightforward and easy to remember. See also notation.
Rows are numbered 1 through 9 from the top row to the bottom row as shown here.
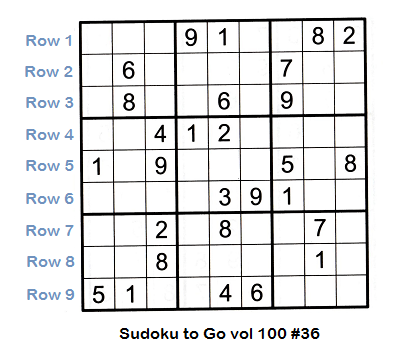
Columns are numbered 1 through 9 from the left column to the right column as shown below.
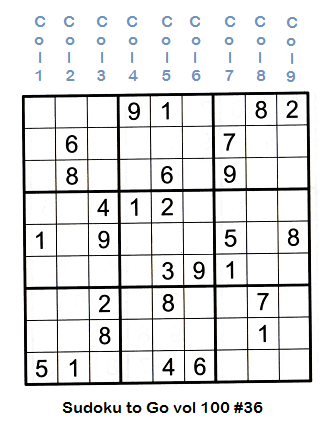
Boxes are numbered 1 through 9 from the top left to the bottom right. See below.
Eight Sudoku Myths debunked > >
Sudoku Patterns
A sudoku pattern is a combination of filled and unfilled cells in a box. Patterns are not fundamental to solving Sudoku but they can help you solve them.
SudokuPrimer has a whole series of patterns that can help you solve puzzles. You can learn how to use each pattern on this website.
Sudoku Pencil Marks
Pencil marks is a sudoku notation scheme where numbers in each cell are written to keep track of each possible number for the given cell. Some or all candidates can be written but writing all candidates is both time-consuming and messy. Snyder Notation is a modified way of writing some candidates, that is superior to writing all of them.
Pencil marks are also often called candidates, and sometimes called little numbers.
Proper Sudoku Puzzle
Sudoku puzzles are "proper" if they only have one solution. A proper puzzle is also called a well-formed sudoku puzzle.
Puzzle setters always want to make sure their puzzles can't have more than one "answer" or solution. There are websites that will tell you if a given puzzle is well-formed.
Sudoku Puzzle Setter
A sudoku puzzle setter is one who creates sudoku puzzles.
Sudoku Rotational Symmetry
Many sudoku puzzles start with a pattern of givens that have "rotational symmetry." This means that if you rotate the puzzle 180 degrees, givens will be in the same positions as before the puzzle was rotated.
See also Fully Symmetrical Sudoku Puzzles.
Here is an example of a puzzle that is rotationally symmetrical.
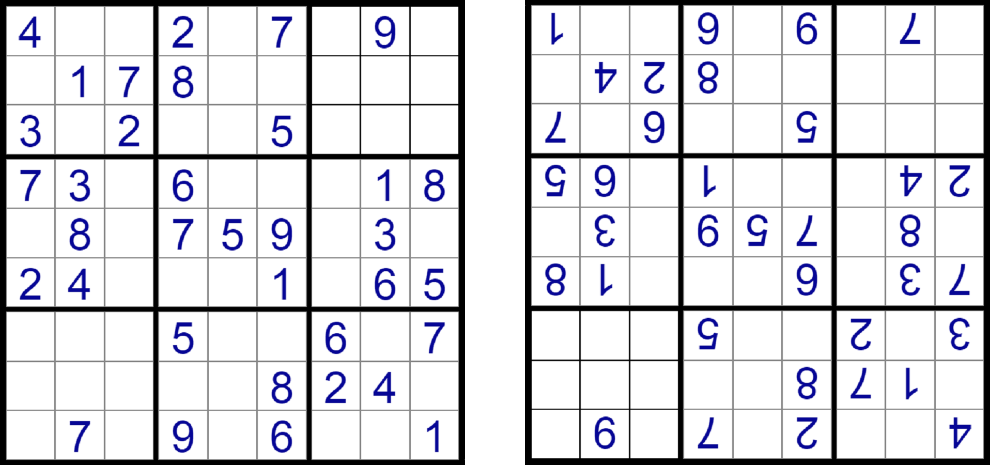
The puzzle on the right is the same puzzle as the one on the left, rotated 180 degrees. If you compare the two images you will see that, although the numbers are upside down on the right image, they are all in the same positions as the numbers in the image on the left.
"Scanning" for Symmetry
Or
Sudoku Symmetry Test
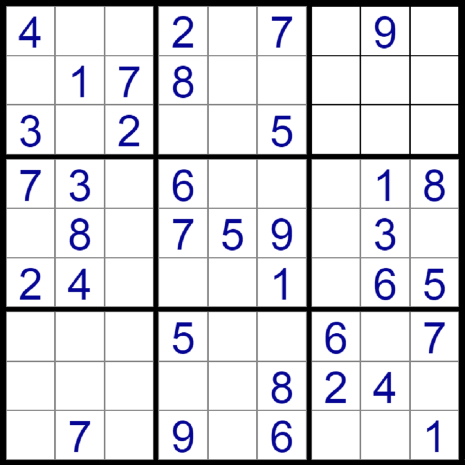
Scanning to see if a puzzle has rotational symmetry is relatively easy. Look at the single puzzle above and see if you can determine whether it is rotationally symmetrical.
Start with box 1 and compare it to box 9. See if they have givens in the same positions. When you do this you need to make sure you imagine box 9 upside down. For example, the 4 in box 1 is in the same position as the 1 in box 9. The 1 in box 1 is in the middle cell so the middle cell in box 9 is its "complement." Therefore the 1 in box 1 is in the same position as the 4 in box 9. As you go on, 3 and 7 are in complement positions, 7 and 2 are in complement positions, and 2 and 6 are in complement positions.
From this scan we have determined that box 1 and box 9 meet the rotational symmetry "test." Now look at box 2 and compare it with box 8 by scanning it in the same way as we did box 1 and 9. If those two boxes pass the "test" check box 3 with box 7, then box 4 with box 6.
At this point you have checked all of the boxes except box 5. Box 5 is a special case. Since it is in the middle of the puzzle it doesn't have a complement box. However, the givens in it must be compared to other givens in the same box. The 6 in r4c4 indicates that another number must be in r6c6. There is a 1 in r6c6 so that passes. Continue to check all givens in box 5 to determine if it passes the "test."
Note that the 5 in r5c5 stands alone. It is in the exact middle of the puzzle and therefore doesn't have a complement. Whether there is a number in r5c5 or not doesn't matter - if the rest of the puzzle is symmetrical, it is symmetrical regardless whether 4r5c5 has a number or not.
If all boxes pass the test and the center box passes the test we have determined that the puzzle is rotationally symmetrical.
Sudoku Row
A sudoku row is a horizontal series of nine adjacent cells. Each row holds the numbers 1 through 9. Every number exists in each row and no number repeats. Rows are one of the three container types.
Create & print your own wordoku puzzles > >
Sudoku Skill Levels
Sudoku puzzles have different skill levels, and solvers have varying levels of skills. Puzzle publishers decide what the skill level is for each published puzzle. Skill levels are therefore quite subjective. Most solvers believe publishers rank their puzzles easier than the stated skill level. In other words, solvers believe that puzzles are easier than they should be based on the stated skill level.
The following are some of the skill levels given on puzzles, roughly from the easiest to the most difficult puzzles.
- Breezy
- Easy
- Medium
- Hard
- Tough
- Difficult
- Expert
- Diabolical
- Extreme
Solvers try puzzles with different skill levels and decide which level they are comfortable at solving. This is the best strategy because of the wide range of levels and difficulties decided on by the publishers.
Snyder Notation
Sudoku Snyder Notation is a system of notating or writing candidates but limiting them to cells which only have two possible numbers. This system of notation is deemed superior to full candidate writing because it gives you helpful information but doesn't require full notation. The benefits are
- it is far less time-consuming
- the puzzle doesn't get as messy
See also candidates, pencil marks
Wayne Gould
Known as the person who made sudoku popular throughout the world.
A retired judge from Hong Kong, Wayne Gould found a sudoku book in Tokyo in 1997 and was fascinated by the puzzle. He spent the next six years writing a computer program called Pappocom Sudoku, which he used to generate sudoku puzzles. In 2004 he convincecd The London Times to publish the puzzles. He also got the Conway Daily Sun in New Hampshire to publish his puzzles.
From there, his puzzles were published by many other UK newspapers. By 2006, sudoku was popular all over the world, thanks to Wayne Gould. Wayne Gould was named "One of the World's Most Influential People" in 2006 by Time Magazine.
Sudoku history is quite fascinating. Read all about sudoku's history.
Well-Formed Sudoku Puzzle
Sudoku puzzles are "well-formed" if they only have one solution. Well-formed puzzles are also called a proper sudoku puzzle.
Puzzle setters always want to make sure their puzzles can't have more than one "answer" or solution. There are websites that will tell you if a given puzzle is well-formed.
If Sudoku Primer and the YouTube channel have helped you, consider donating a little

Thanks in advance for your support!
More About Sudoku
Sudoku - the puzzle that addicts
