Tool: Sudoku Double Row/Column Elimination

---

<< Return to techniques page

Next technique: loner cells >>

Introduction

Using this technique you can often solve a single number. There are other times when you can't solve a number but you can constrain a number to one row or column.

Once you have learned how to spot these you will start noticing them quite often. You can also find two or more of these in the same puzzle that are related.

Details

Double row & column elimination is where a given number is known to only be able to reside in two rows or two columns in two boxes.

The First Example

Look at figure 1. The 7 in box 3 can only reside in either r3c7 or r3c8 (circled green). Another way to say it is the 7 Must be in c7 or c8 in box 3.

Even though we can't determine which column holds the 7 in box 3, we still know that the 7 cannot reside in column 9.

If we can find another box below box 3 that has the same situation where the 7 can only be in c7 or c8 then we will know that the 7 must reside in c9 in the remaining box.

Now look at box 6. The 7 in this box must reside in row 4 and therefore it can only be in c7 or c8 (circled green), the same as box 3. So now we have two boxes where the 7 can only reside in c7 or c8. The 7s in those two boxes 'cancel each other out' so to speak. That means in box 9 the 7 cannot be in c7 or c8 and therefore must reside in c9 (circled red).

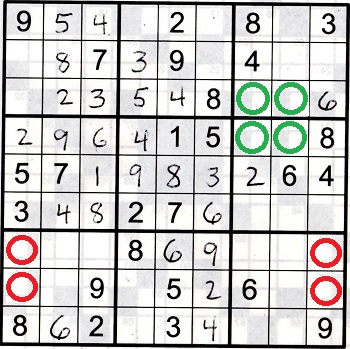
figure 1

The Second Example

Look at the 17 twins in box 8. We can't solve them yet. But let's see if double row elimination can help.

We determined in the first example that the 7 in box 9 is either in r7c9 or r8c9. In box 7, the 7 can only be in r7c1 or r8c1 (circled red). That covers r7 and r8. So the 7 in box 8 must be in r9. Using double row elimination solved the 17 twins in box 8.

Skill Levels

Double row & column elimination is useful on medium to hard puzzles.

Next technique: loner cells >>

<< Return to techniques page

---