Tool: Sudoku Ambiguity rule

Also Called Sudoku Unique Rectangles

---

<< Return to techniques page

Next technique: solving single cells >>

Introduction

When Sudoku puzzles are created the designers make sure that there is one and only one solution to a given puzzle. This means that you can not solve it in more than one way. In fact, by definition, a sudoku puzzle is not a sudoku puzzle unless it only has one solution.

Every cell in the puzzle can only have one of the nine numbers in it to be solved correctly. If a given cell has a 5 in it, for example, the puzzle cannot be correctly solved with any other number in that cell.

One strategy for designing a puzzle is to selectively remove numbers and then try to solve the puzzle with the remaining numbers. During this process the designer must be careful not to remove two numbers that would cause an ambiguity (where those two numbers could be swapped and the puzzle could be completed two different ways, therefore having two solutions).

This is what is called the sudoku ambiguity rule. Many puzzle solvers call this situation sudoku Unique Rectangles, or sudoku UR for short.

Details

We can take advantage of this and use it to give us clues about where numbers can go. Look at the following puzzle. The four cells that are circled are a place where we can use the ambiguity rule.

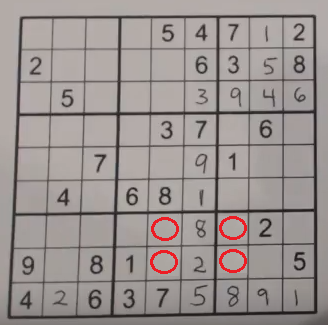
Puzzle #88 from Sudoku To Go volume 103 by Soap Opera Digest

Now let's look at this puzzle and see what is possible in these cells.

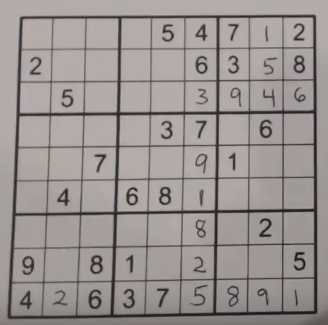
Box 8 has three empty cells and is missing 469. With the obvious clues we have the 4 can fit in any empty cell. The 6 can only fit in column 5 (because of the 6 in box 5) and the 9 can only fit in r7 (because of the 9 in box 7).

Now look at box 9 - it has two sets of twins that can't be solved yet, but we know they are twins. There are 37 twins in r7c9 and r8c8 (because of the 3 and 7 already in column 7) and therefore there are 46 twins in the other two empty cells r7c7 and r8c7. The 46 twins will help us find where the 4 fits in box 8.

With that knowledge let's look at box 8 again. Since the 6 can only fit in column 5 we cannot have a 4 in column 5 because we would then have 46 twins in both b8 and b9 in row 7 and row 8. If that were the case, either box (box 8 or box 9) could have the 4 above the 6 or the 4 below the 6 (and the opposite in the other box), which would give the puzzle two solutions.

Therefore, because of this rule, the 4 must fit in r7c4. See the image below for the correct placement of the 4 in b8.

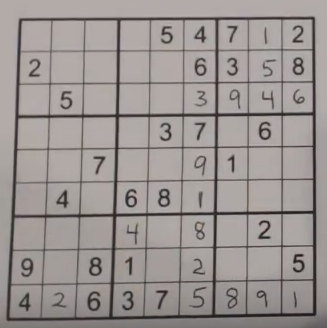
Skill Levels

This advanced technique is most useful on hard and diabolical puzzles. It could certainly be used on easier puzzles but there are probably easier techniques that will stand out ahead of this rule, since the ambiguity rule is harder to spot.

Take Note

It is recommended that you get very familiar with the ambiguity rule. As you learn this rule, you will start to spot URs in puzzles. You will then start to see them more and more because they are more prevalent than first thought.

When solving very difficult puzzles there will be times when this technique is the only thing you will find, to get you past an otherwise unsolvable puzzle. It is very useful and powerful when you know how to use it.

Next technique: solving single cells >>

<< Return to techniques page

---