---

---

If Sudoku Primer and the YouTube channel have helped you, consider donating a little



Thanks in advance for your support!

---

Sudoku Challenge Hard #1 solution

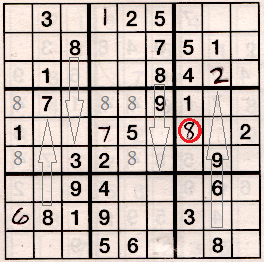
Take a look at the middle horizontal section, boxes 4 through 6. Note that box 4 can only have 8's in column 1. The 8's are in row 4 and 6. These are called "ghost 8's" and are grey to indicate that 8's are possible in either of the cells where a grey 8 resides but only one cell can actually have an 8.

Now look at the middle box (box 5). it can't have 8's in column 6. But 8's are possible in column 5 and an 8 is possible in column 4. It therefore has three "ghost 8's."

Even though we don't know yet which of the ghost 8's are the real 8's they often eliminate rows and columns. In this challenge they eliminate two of the three rows in the middle section.

Looking at both the left and middle boxes together (boxes 4 and 5) you will see that neither box can have an 8 anywhere in row 5. Because of that the 8 in the right box (box 6) must be in row 5, and you see that the only available place for an 8 in row 5 is the left-most cell.

This is what is called "double row elimination." It can also be used in columns. It is very powerful and can be found quite often in harder puzzles. When you learn to see this combination you will be able to fill in more numbers in harder puzzles.

Additional Challenge

To help solidify the concept of "double row/column elimination" do this additional activity: In this puzzle you will see another "double row elimination." See if you can find it. Hint: it contains the number 2.

Good luck!

---

If Sudoku Primer and the YouTube channel have helped you, consider donating a little



Thanks in advance for your support!

---

More About Sudoku

---

---

Sudoku - the puzzle that addicts